This python script trains a simple naive Bayes classifier on training.csv, classifies the events in test.csv, and creates a file called submission.csv that you can submit at the Kaggle submission site. You can execute this standalone python script (in the directory where you copied training.csv and test.csv), you can execute this iPython notebook, or you can read the same notebook below (or here in a nicer format).
Starting kit for the Higgs boson machine learning challenge¶
This notebook contains a starting kit for the Higgs boson machine learning challenge. Download the training set (called training.csv) and the test set (test.csv), then execute cells in order.
import random,string,math,csv
import numpy as np
import matplotlib.pyplot as pltReading an formatting training data¶
all = list(csv.reader(open("training.csv","rb"), delimiter=','))Slicing off header row and id, weight, and label columns.
xs = np.array([map(float, row[1:-2]) for row in all[1:]])
(numPoints,numFeatures) = xs.shapePerturbing features to avoid ties. It's far from optimal but makes life easier in this simple example.
xs = np.add(xs, np.random.normal(0.0, 0.0001, xs.shape))Label selectors.
sSelector = np.array([row[-1] == 's' for row in all[1:]])
bSelector = np.array([row[-1] == 'b' for row in all[1:]])Weights and weight sums.
weights = np.array([float(row[-2]) for row in all[1:]])
sumWeights = np.sum(weights)
sumSWeights = np.sum(weights[sSelector])
sumBWeights = np.sum(weights[bSelector])Training and validation cuts¶
We will train a classifier on a random training set for minimizing the weighted error with balanced weights, then we will maximize the AMS on the held out validation set.
randomPermutation = random.sample(range(len(xs)), len(xs))
numPointsTrain = int(numPoints*0.9)
numPointsValidation = numPoints - numPointsTrain
xsTrain = xs[randomPermutation[:numPointsTrain]]
xsValidation = xs[randomPermutation[numPointsTrain:]]
sSelectorTrain = sSelector[randomPermutation[:numPointsTrain]]
bSelectorTrain = bSelector[randomPermutation[:numPointsTrain]]
sSelectorValidation = sSelector[randomPermutation[numPointsTrain:]]
bSelectorValidation = bSelector[randomPermutation[numPointsTrain:]]
weightsTrain = weights[randomPermutation[:numPointsTrain]]
weightsValidation = weights[randomPermutation[numPointsTrain:]]
sumWeightsTrain = np.sum(weightsTrain)
sumSWeightsTrain = np.sum(weightsTrain[sSelectorTrain])
sumBWeightsTrain = np.sum(weightsTrain[bSelectorTrain])xsTrainTranspose = xsTrain.transpose()Making signal and background weights sum to 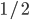 each to emulate uniform priors
each to emulate uniform priors 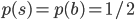 .
.
weightsBalancedTrain = np.array([0.5 * weightsTrain[i]/sumSWeightsTrain
if sSelectorTrain[i]
else 0.5 * weightsTrain[i]/sumBWeightsTrain\
for i in range(numPointsTrain)])Training naive Bayes and defining the score function¶
Number of bins per dimension for binned naive Bayes.
numBins = 10logPs[fI,bI] will be the log probability of a data point x with binMaxs[bI - 1] < x[fI] <= binMaxs[bI] (with binMaxs[-1] = -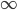 by convention) being a signal under uniform priors
by convention) being a signal under uniform priors 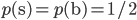 .
.
logPs = np.empty([numFeatures, numBins])
binMaxs = np.empty([numFeatures, numBins])
binIndexes = np.array(range(0, numPointsTrain+1, numPointsTrain/numBins))for fI in range(numFeatures):
# index permutation of sorted feature column
indexes = xsTrainTranspose[fI].argsort()
for bI in range(numBins):
# upper bin limits
binMaxs[fI, bI] = xsTrainTranspose[fI, indexes[binIndexes[bI+1]-1]]
# training indices of points in a bin
indexesInBin = indexes[binIndexes[bI]:binIndexes[bI+1]]
# sum of signal weights in bin
wS = np.sum(weightsBalancedTrain[indexesInBin]
[sSelectorTrain[indexesInBin]])
# sum of background weights in bin
wB = np.sum(weightsBalancedTrain[indexesInBin]
[bSelectorTrain[indexesInBin]])
# log probability of being a signal in the bin
logPs[fI, bI] = math.log(wS/(wS+wB))The score function we will use to sort the test examples. For readability it is shifted so negative means likely background (under uniform prior) and positive means likely signal. x is an input vector.
def score(x):
logP = 0
for fI in range(numFeatures):
bI = 0
# linear search for the bin index of the fIth feature
# of the signal
while bI < len(binMaxs[fI]) - 1 and x[fI] > binMaxs[fI, bI]:
bI += 1
logP += logPs[fI, bI] - math.log(0.5)
return logPOptimizing the AMS on the held out validation set¶
s and b are the sum of signal and background weights, respectively, in the selection region.def AMS(s,b):
assert s >= 0
assert b >= 0
bReg = 10.
return math.sqrt(2 * ((s + b + bReg) *
math.log(1 + s / (b + bReg)) - s))Computing the scores on the validation set
validationScores = np.array([score(x) for x in xsValidation])Sorting the indices in increasing order of the scores.
tIIs = validationScores.argsort()Weights have to be normalized to the same sum as in the full set.
wFactor = 1.* numPoints / numPointsValidationInitializing 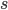 and
and 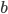 to the full sum of weights, we start by having all points in the selectiom region.
to the full sum of weights, we start by having all points in the selectiom region.
s = np.sum(weightsValidation[sSelectorValidation])
b = np.sum(weightsValidation[bSelectorValidation])amss will contain AMSs after each point moved out of the selection region in the sorted validation set.
amss = np.empty([len(tIIs)])amsMax will contain the best validation AMS, and threshold will be the smallest score among the selected points.
amsMax = 0
threshold = 0.0We will do len(tIIs) iterations, which means that amss[-1] is the AMS when only the point with the highest score is selected.
for tI in range(len(tIIs)):
# don't forget to renormalize the weights to the same sum
# as in the complete training set
amss[tI] = AMS(max(0,s * wFactor),max(0,b * wFactor))
if amss[tI] > amsMax:
amsMax = amss[tI]
threshold = validationScores[tIIs[tI]]
#print tI,threshold
if sSelectorValidation[tIIs[tI]]:
s -= weightsValidation[tIIs[tI]]
else:
b -= weightsValidation[tIIs[tI]]amsMaxthresholdplt.plot(amss)Computing the permutation on the test set¶
Reading the test file, slicing off the header row and the id column, and converting the data into float.
test = list(csv.reader(open("test.csv", "rb"),delimiter=','))
xsTest = np.array([map(float, row[1:]) for row in test[1:]])testIds = np.array([int(row[0]) for row in test[1:]])Computing the scores.
testScores = np.array([score(x) for x in xsTest])Computing the rank order.
testInversePermutation = testScores.argsort()testPermutation = list(testInversePermutation)
for tI,tII in zip(range(len(testInversePermutation)),
testInversePermutation):
testPermutation[tII] = tIComputing the submission file with columns EventId, RankOrder, and Class.
submission = np.array([[str(testIds[tI]),str(testPermutation[tI]+1),
's' if testScores[tI] >= threshold else 'b']
for tI in range(len(testIds))])submission = np.append([['EventId','RankOrder','Class']],
submission, axis=0)Saving the file that can be submitted to Kaggle.
np.savetxt("submission.csv",submission,fmt='%s',delimiter=',')